type
status
date
slug
summary
tags
category
icon
password
网址
📝 算法解释
深度优先搜索和广度优先搜索是两种最常见的优先搜索方法,它们被广泛地运用在图和树等结构中进行搜索。
深度优先搜索
深度优先搜索(depth-first search,DFS)在搜索到一个新的节点时,立即对该新节点进行遍历;因此遍历需要用先入后出的栈(stack)来实现,也可以通过与栈等价的递归来实现。对于树结构而言,由于总是对新节点调用遍历,因此看起来是向着“深”的方向前进。在 Python 中,我们可以用 collections.deque 来实现 C++ 中的 stack。但是通常情况下,我们还是会选用 C++ 中的vector 或 Python 中的 list 来实现栈,因为它们既是先入后出的数据结构,又能支持随机查找。

考虑如下一颗简单的树,我们从 1 号节点开始遍历。假如遍历顺序是从左子节点到右子节点,那么按照优先向着“深”的方向前进的策略,则遍历过程为 1(起始节点)->2(遍历更深一层的左子节点)->4(遍历更深一层的左子节点)->2(无子节点,返回父结点)->1(子节点均已完成遍历,返回父结点)->3(遍历更深一层的右子节点)->1(无子节点,返回父结点)-> 结束程序(子节点均已完成遍历)。如果我们使用栈实现,我们的栈顶元素的变化过程为 1->2->4->3。
深度优先搜索也可以用来检测环路:记录每个遍历过的节点的父节点,若一个节点被再次遍历且父节点不同,则说明有环。我们也可以用之后会讲到的拓扑排序判断是否有环路,若最后存在入度不为零的点,则说明有环。
有时我们可能会需要对已经搜索过的节点进行标记,以防止在遍历时重复搜索某个节点,这种做法叫做状态记录或记忆化(memoization)。
695. 岛屿的最大面积
题目描述
给定一个二维的 0-1 矩阵,其中 0 表示海洋,1 表示陆地。单独的或相邻的陆地可以形成岛屿,每个格子只与其上下左右四个格子相邻。求最大的岛屿面积。
输入输出样例
输入是一个二维数组,输出是一个整数,表示最大的岛屿面积
题解
此题是十分标准的搜索题,我们可以拿来练手深度优先搜索。一般来说,深度优先搜索类型的题可以分为主函数和辅函数,主函数用于遍历所有的搜索位置,判断是否可以开始搜索,如果可以即在辅函数进行搜索。辅函数则负责深度优先搜索的递归调用。当然,我们也可以使用栈(stack)实现深度优先搜索,但因为栈与递归的调用原理相同,而递归相对便于实现,因此刷题时笔者推荐使用递归式写法,同时也方便进行回溯(见下节)。不过在实际工程上,直接使用栈可能才是最好的选择,一是因为便于理解,二是更不易出现递归栈满的情况。
我们先展示使用栈的写法。这里我们使用了一个小技巧,对于四个方向的遍历,可以创造一个数组 [-1, 0, 1, 0, -1],每相邻两位即为上下左右四个方向之一。当然您也可以显式写成 [-1, 0]、[1, 0]、[0, 1] 和 [0, -1],以便理解
547. 省份数量
题目描述
给定一个二维的 0-1 矩阵,如果第 (i, j) 位置是 1,则表示第 i 个城市和第 j 个城市处于同一城市圈。已知城市的相邻关系是可以传递的,即如果 a 和 b 相邻,b 和 c 相邻,那么 a 和 c 也相邻,换言之这三个城市处于同一个城市圈之内。求一共有多少个城市圈。
输入输出样例
输入是一个二维数组,输出是一个整数,表示城市圈数量。因为城市相邻关系具有对称性,该二维数组为对称矩阵。同时,因为自己也处于自己的城市圈,对角线上的值全部为 1。
题解
在上一道题目中,图的表示方法是,每个位置代表一个节点,每个节点与上下左右四个节点相邻。而在这一道题里面,每一行(列)表示一个节点,它的每列(行)表示是否存在一个相邻节点。上一道题目拥有 m × n 个节点,每个节点有 4 条边;而本题拥有 n 个节点,每个节点最多有 n 条边,表示和所有城市都相邻,最少可以有 1 条边,表示当前城市圈只有自己。当清楚了图的表示方法后,这道题目与上一道题目本质上是同一道题:搜索城市圈(岛屿圈)的个数。我们这里采用递归的写法。
注意 对于节点连接类问题,我们也可以利用并查集来进行快速的连接和搜索。
417. 太平洋大西洋水流问题
题目描述
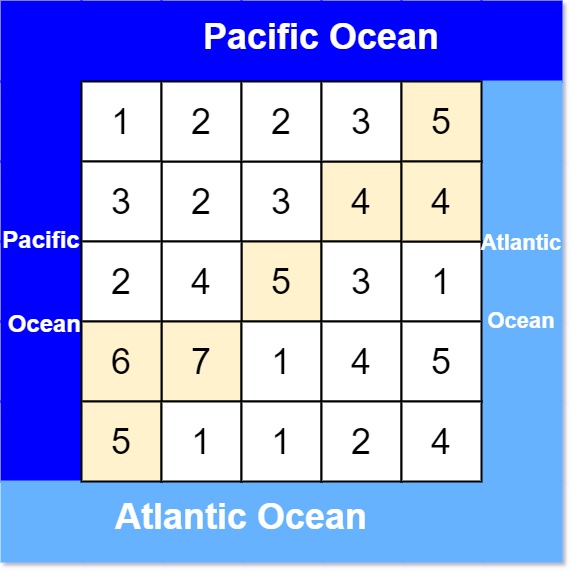
给定一个二维的非负整数矩阵,每个位置的值表示海拔高度。假设左边和上边是太平洋,右边和下边是大西洋,求从哪些位置向下流水,可以流到太平洋和大西洋。水只能从海拔高的位置流到海拔低或相同的位置。
输入输出样例
输入是一个二维的非负整数数组,表示海拔高度。输出是一个二维的数组,其中第二个维度大小固定为 2,表示满足条件的位置坐标。
示例 :
题解
虽然题目要求的是满足向下流能到达两个大洋的位置,如果我们对所有的位置进行搜索,那
么在不剪枝的情况下复杂度会很高。因此我们可以反过来想,从两个大洋开始向上流,这样我们
只需要对矩形四条边进行搜索。搜索完成后,只需遍历一遍矩阵,两个大洋向上流都能到达的位
置即为满足条件的位置。
回溯法
回溯法(backtracking)是优先搜索的一种特殊情况,又称为试探法,常用于需要记录节点状态的深度优先搜索。通常来说,排列、组合、选择类问题使用回溯法比较方便。顾名思义,回溯法的核心是回溯。在搜索到某一节点的时候,如果我们发现目前的节点(及其子节点)并不是需求目标时,我们回退到原来的节点继续搜索,并且把在目前节点修改的状态还原。这样的好处是我们可以始终只对图的总状态进行修改,而非每次遍历时新建一个图来储存状态。在具体的写法上,它与普通的深度优先搜索一样,都有 [修改当前节点状态]→[递归子节点] 的步骤,只是多了回溯的步骤,变成了 [修改当前节点状态]→[递归子节点]→[回改当前节点状态]。
没有接触过回溯法的读者可能会不明白我在讲什么,这也完全正常,希望以下几道题可以让您理解回溯法。如果还是不明白,可以记住两个小诀窍,一是按引用传状态,二是所有的状态修改在递归完成后回改。
回溯法修改一般有两种情况,一种是修改最后一位输出,比如排列组合;一种是修改访问标记,比如矩阵里搜字符串。
46. 全排列
题目描述
给定一个无重复数字的整数数组,求其所有的排列方式。
输入输出样例
输入是一个一维整数数组,输出是一个二维数组,表示输入数组的所有排列方式。
题解
怎样输出所有的排列方式呢?对于每一个当前位置 i,我们可以将其于之后的任意位置交换,然后继续处理位置 i+1,直到处理到最后一位。为了防止我们每此遍历时都要新建一个子数组储存位置 i 之前已经交换好的数字,我们可以利用回溯法,只对原数组进行修改,在递归完成后再修改回来。我们以样例 [1,2,3] 为例,按照这种方法,我们输出的数组顺序为 [[1,2,3], [1,3,2], [2,1,3], [2,3,1],[3,2,1], [3,1,2]],可以看到所有的排列在这个算法中都被考虑到了。
77. 组合
题目描述
给定一个整数 n 和一个整数 k,求在 1 到 n 中选取 k 个数字的所有组合方法。
输入输出样例
输入是两个正整数 n 和 k,输出是一个二维数组,表示所有组合方式。
题解
类似于排列问题,我们也可以进行回溯。排列回溯的是交换的位置,而组合回溯的是是否把当前的数字加入结果中。
79. 单词搜索
题目描述
给定一个字母矩阵,所有的字母都与上下左右四个方向上的字母相连。给定一个字符串,求字符串能不能在字母矩阵中寻找到。
输入输出样例
输入是一个二维字符数组和一个字符串,输出是一个布尔值,表示字符串是否可以被寻找
到。
从左上角的’A’ 开始,我们可以先向右、再向下、最后向左,找到连续的"ABCCED"。
题解
不同于排列组合问题,本题采用的并不是修改输出方式,而是修改访问标记。在我们对任意位置进行深度优先搜索时,我们先标记当前位置为已访问,以避免重复遍历(如防止向右搜索后又向左返回);在所有的可能都搜索完成后,再回改当前位置为未访问,防止干扰其它位置搜索到当前位置。使用回溯法时,我们可以只对一个二维的访问矩阵进行修改,而不用把每次的搜索状态作为一个新对象传入递归函数中。
51. N 皇后
题目描述

给定一个大小为 n 的正方形国际象棋棋盘,求有多少种方式可以放置 n 个皇后并使得她们互不攻击,即每一行、列、左斜、右斜最多只有一个皇后。
输入输出样例
输入是一个整数 n,输出是一个二维字符串数组,表示所有的棋盘表示方法。
题解
类似于在矩阵中寻找字符串,本题也是通过修改状态矩阵来进行回溯。不同的是,我们需要对每一行、列、左斜、右斜建立访问数组,来记录它们是否存在皇后。这里如果我们通过对每一行/列遍历来插入皇后,我们就不需要对行/列建立访问数组了。
广度优先搜索
广度优先搜索(breadth-first search,BFS)不同与深度优先搜索,它是一层层进行遍历的,因此需要用先入先出的队列 (queue) 而非先入后出的栈 (stack) 进行遍历。由于是按层次进行遍历,广度优先搜索时按照“广”的方向进行遍历的,也常常用来处理最短路径等问题。在 Python 中,
我们可以用 collections.deque 来实现 C++ 中的 queue。考虑如下一颗简单的树。我们从 1 号节点开始遍历,假如遍历顺序是从左子节点到右子节点,那么按照优先向着“广”的方向前进的策略,队列顶端的元素变化过程为 [1]->[2->3]->[4],其中方括号代表每一层的元素。

这里要注意,深度优先搜索和广度优先搜索都可以处理可达性问题,即从一个节点开始是否能达到另一个节点。因为深度优先搜索可以利用递归快速实现,很多人会习惯使用深度优先搜索刷此类题目。实际软件工程中,笔者很少见到递归的写法,因为一方面难以理解,另一方面可能产生栈溢出的情况;而用栈实现的深度优先搜索和用队列实现的广度优先搜索在写法上并没有太大差异,因此使用哪一种搜索方式需要根据实际的功能需求来判断。另外,如果需要自定义搜索优先级,我们可以利用优先队列。
1091. 二进制矩阵中的最短路径
题目描述
给定一个二维 0-1 矩阵,其中 1 表示障碍,0 表示道路,每个位置与周围八个格子相连。求从左上角到右下角的最短到达距离。如果没有可以到达的方法,返回-1。
输入输出样例
输入是一个二维整数数组,输出是一个整数,表示最短距离
最短到达方法为先向右,拐弯之后再向下
题解
利用队列,我们可以很直观地利用广度优先搜索,搜索最少扩展层数,即最短到达目的地的
距离。注意不要重复搜索相同位置。
解题步骤(BFS 框架)
- 边界检查:如果起点或终点是 1,返回 -1。
- 初始化:
- n = len(grid)。
- 8 个方向:directions = [(-1,-1), (-1,0), (-1,1), (0,-1), (0,1), (1,-1), (1,0), (1,1)]。
- visited: n×n 布尔矩阵,标记已访问(防止重复入队)。
- queue: 使用 deque,初始放入起点 (0,0,1)(位置 + 当前长度)。
- BFS 循环:
- while queue:
- 出队当前 (i, j, length)。
- 如果是终点,返回 length。
- 尝试 8 个方向:
- 新位置 (ni, nj) 在界内、是 0、未访问 → 标记 visited[ni][nj]=True,入队 (ni, nj, length+1)。
- 结束:队列空仍未到终点,返回 -1。
934. 最短的桥
题目描述
给定一个二维 0-1 矩阵,其中 1 表示陆地,0 表示海洋,每个位置与上下左右相连。已知矩阵中有且只有两个岛屿,求最少要填海造陆多少个位置才可以将两个岛屿相连。
输入输出样例
输入是一个二维整数数组,输出是一个非负整数,表示需要填海造陆的位置数
题解
本题实际上是求两个岛屿间的最短距离,因此我们可以先通过任意搜索方法找到其中一个岛屿,然后利用广度优先搜索,查找其与另一个岛屿的最短距离。这里我们展示利用深度优先搜索查找第一个岛屿。
这个题目要求在 n×n 二元矩阵(1=陆地,0=水域)中连接两个不相连的岛(岛由四个方向相连的 1 组成),通过翻转最少的 0 为 1 来形成一座岛。输出最小翻转数(即连接两个岛的最短“桥”长度,桥是中间的 0 数量)。
为什么用 BFS + DFS?
- 核心思想:先用 DFS 找到第一个岛的所有陆地点(标记 visited 并放入 BFS 队列,作为起点,初始距离 0)。然后用 BFS 从这些陆地扩展,探索相邻的 0(每步翻转一个 0,距离 +1),直到碰到第二个岛的陆地(未标记的 1),此时距离就是最小桥长。
- 为什么有效?
- DFS 高效收集第一个岛(O(n^2) 最坏,但 n≤100)。
- BFS 保证最短路径(层级扩展,从一个岛“扩散”到另一个,第一次碰到第二个岛就是最近距离)。
- 四个方向(上、下、左、右),无对角。
- 时间/空间:O(n^2),每个格子访问最多一次。
- 注意:矩阵恰有两个岛,不相连;起点/终点无需特殊处理。
解题步骤
- 初始化:visited = [[False]*n for _ in range(n)],dirs = [(-1,0),(1,0),(0,-1),(0,1)],q = deque()。
- 找第一个岛:遍历 grid,遇到第一个 1,调用 DFS 标记所有连通 1 为 visited=True,并加入 q(dist=0)。
- BFS 扩展:
- while q:出队 (i,j,dist)。
- 四个方向:新位置 (ni,nj) 在界内且未 visited。
- 如果 grid[ni][nj] == 1:那是第二个岛,返回 dist(桥长)。
- 否则(是 0):标记 visited=True,入队 (ni,nj, dist+1)。
- 结束:理论上总能找到(两个岛),但代码安全。
🤗 练习
130. 被围绕的区域
这个题目是一个经典的图遍历 + 原地修改问题,考察对连通区域的识别和处理。矩阵中 'O' 代表空地,'X' 代表障碍。我们需要找出那些完全被 'X' 包围的 'O' 区域(即无法逃到边界),并将它们捕获(改为 'X')。关键是“包围”:一个 'O' 区域如果能通过上下左右相连到达矩阵边缘,就不算被包围(因为它能“逃脱”)。
为什么难?核心挑战
- 连通性:'O' 区域是四个方向(上、下、左、右)相连的“岛屿”,不能对角。
- 原地修改:不能用额外空间复制矩阵,直接改 board。
- 边界特殊:边缘的 'O' 永远不被捕获,因为它们“触边”了。
- 规模:m,n ≤ 200,O(m*n) 时间/空间 OK,递归 DFS 栈深 ≤ 40000(Python 默认够用)。
直观:暴力 DFS 每个 'O' 检查包围太慢(O((mn)^2))。聪明办法:反向思维,从边界 'O' 开始标记所有“安全”区域(能逃脱的),然后捕获剩下的。
解题思路(DFS + 标记)
- 从边界遍历:检查 board 的四条边上所有 'O',对每个边界 'O' 调用 DFS,将其连通的整个 'O' 区域临时标记为其他字符(如 'A',表示“安全,不能捕获”)。
- DFS 原理:从当前 (i,j) 扩展到四个方向,如果是 'O' 且在界内,就标记为 'A' 并递归。
- 全局捕获:遍历整个矩阵,将所有剩余的 'O' 改为 'X'(这些是被包围的)。
- 恢复:将所有 'A' 改回 'O'(安全区域恢复原样)。
- 为什么从边界开始? 所有能逃脱的 'O' 最终都会连通到边界,先标记它们,避免误捕获。
- 时间/空间:O(mn),每个格子访问常数次。空间 O(mn) 最坏(递归栈),但实际小。
257. 二叉树的所有路径
47. 全排列 II
全排列 II 是经典回溯(Backtracking)问题,基于 LeetCode 46(全排列)的扩展。核心是生成数组 nums 的所有唯一排列(无重复),数组可能有重复元素。输出所有不重复的排列序列。
问题分析
- 无重复时(如 [1,2,3]):有 n! 个排列。
- 有重复时(如 [1,1,2]):直接回溯会产生重复(如 [1,1,2] 和另一个 [1,1,2]),需去重。
- 约束:n ≤ 8,小规模,回溯 O(n!) 可接受(8! = 40320)。
- 关键挑战:避免重复排列。排序后 + 剪枝:跳过与前一个相同且前一个未用的元素。
为什么用回溯?
- 回溯框架:从空路径开始,逐位选择未用元素,递归构建路径,到长度 n 时添加结果,回溯撤销选择。
- 处理重复:
- 先 sort(nums),相同元素相邻。
- 在 for 循环选择 i 时:如果 nums[i] == nums[i-1] 且 used[i-1] == False(前一个相同元素未用,意味着它被“跳过”了),则 skip i(避免从这里开始的重复分支)。
- 标记:用 used 布尔数组记录元素是否用过(因为交换 nums 会乱序,用 used 更稳)。
解题步骤
- 预处理:排序 nums,初始化 res = [],used = [False] * n。
- 回溯函数 backtrack(path, used):
- 终止:len(path) == n → res.append(path[:])(复制路径,避免引用)。
- 选择:for i in 0..n-1:
- if used[i]:continue。
- 去重剪枝:if i > 0 and nums[i] == nums[i-1] and not used[i-1]:continue。
- 标记 used[i]=True,path.append(nums[i])。
- 递归 backtrack(path, used)。
- 回溯:path.pop(),used[i]=False。
- 返回 res。
- Author:无敌宝宝男sp
- URL:http://www.wudibaobaoda.top/article/2864032f-33bf-80d7-b946-dd9a128f0e87
- Copyright:All articles in this blog, except for special statements, adopt BY-NC-SA agreement. Please indicate the source!
























